Golden Sections
I often look at the “golden section grid” when analyzing a painting. I’ll describe it below – the further you read the more math will crop up. So, start at the top for the summary and quit reading whenever you feel like it.
The Not-So-Math Part
When it gets right down to it, certain proportions just look better to us. No one knows why, exactly, but folks as far back as ancient Greece and Egypt recognized the fact and worked out guidelines to help us use those proportions. One of the most important of these guidelines is the so-called “golden section.”
Proportions are all about relationships. How do the parts look compared to each other, and compared to the whole? How long, how tall, how wide? In math, we talk about relationship and proportion by using ratios. The golden section, also called the golden ratio, is:
1 to 1.6180…
So, if you have a rectangle that is 1 foot tall, that rectangle is “golden” if it is 1.6180 feet wide. It’s not the only rectangle that looks good, but it’s one of the most useful. You don’t need to understand the mathematics, but if you want to know I’ll go into some of that below. For some, though, it’s enough to know the golden ratio itself to use it in their art. In the end, even going through the math doesn’t tell you why it works. But it can increase your appreciation.
Before getting to that though, I have one other point to make. If you have a line, like the side of a rectangle, you can divide that line into two sections according to the golden ratio. So, if your line is 100 cm long, you can divide it into two line segments of approximately 38 and 62 cm.
62 : 100 is the ratio of the longer line to the whole thing. It reduces down to 1 : 1.6180.
38: 62 is the ratio of the shorter line to the longer line. It also reduces down to 1 : 1.6180.
If that 100 cm is the side of a rectangle, and that rectangle happens to be your painting canvas, putting things along those lines at 38 and 62 cm will just naturally look right. Then, if you do the same thing along the bottom and top of your rectangle, and draw the lines at those golden section divisions, you’ll end up with a grid of 9 rectangles inside your overall canvas, like this:
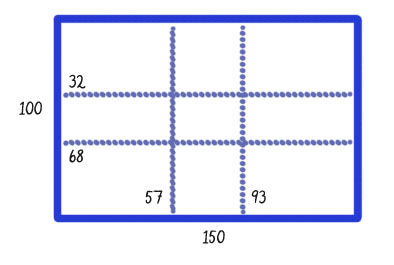
A 100 x 150 rectangle divided up according to the golden ratio.
Placing things along those lines, and especially at the intersections of the lines, will result in a more pleasing composition than you’ll get with just about any other method.
Slightly Mathier Parts
So where did this magic number of 1.6180 come from? For one thing, it’s known as Phi (ϕ) and it’s one of those numbers like Pi where the decimals go on forever. One of its sources is the Fibonacci sequence. If you start with 0 and 1, you get the next number of the sequence by adding the last two. So:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
You can find examples of this sequence all through nature. Tool uses it in their song Lateralus – look at the syllable counts for the first couple parts of the song.
It’s quite approximate at first, but if you take any two consecutive numbers in the sequence and divide the smaller one into the larger, you get a number very close to Phi. So that’s one of the ways that artists and mathematicians got to the golden rectangle.
I’ll have more to say on this soon, but for now I’ll stop here. When I get more time I’ll go into the relationships between the golden rectangle and some of the other rectangles in Dynamic Symmetry. Until then, see the analysis on Maxfield Parrish.